Dreiecksmessung
Allgemein gilt für die Flächenberechnung eines Dreiecks die Formel A = g∙h/2, wobei A für die Fläche, g für die Grundseite und h für die Höhe steht. Die Höhe h wird in der Geometria Culmensis Mitteldrebom genannt. Diesen Mitteldrebom kann man mit Meßwerkzeugen messen oder rechnerisch ermitteln.
Die Fläche von rechtwinkligen Dreiecken wird berechnet indem man die beiden Seiten, die den rechten Winkel einschließen, multipliziert und davon die Hälfte nimmt. Der Verfasser der Geometria Culmensis bezieht sich hier auf die 34. Proposition im I. Buch Euklids:
Im Parallelogramm sind gegenüberliegende Seiten bzw. Winkel gleich, jede Diagonale zerlegt das Parallelogramm in 2 kongruente Dreiecke.
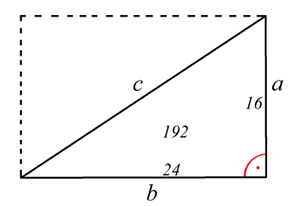
Da ein Rechteck ein spezielles Parallelogramm ist, zerlegt auch hier die Diagonale das Rechteck in zwei flächengleiche rechtwinklige Dreiecke. Für die Fläche des Dreiecks ergibt sich A = a∙b/2 = 16∙24/2 = 192.
Zu den Beziehungen zwischen den drei Seiten eines rechtwinkligen Dreiecks kann man in der Geometria Culmensis folgendes lesen:
Alzo wirt das vierkante velt gemessen vs der langen want alzo gros als dy beyde virkante, dy do werden gemessen von den czwen wenden des geren, dy do czusamene treten in dem rechten wynkel. Dorus man sal wyssen, das der gere vorgelegit yst rechtwinkelik, alz man hy sehen mak yn desir figuren.
Also wird das quadrierte Feld gemessen aus der langen Seite genau so groß wie die beiden Quadrate, gemessen von den zwei Seiten des Dreiecks, die da zusammentreten in dem rechten Winkel. Daraus soll man wissen, dass das vorgelegte Dreieck rechtwinklig ist, als man hier sehen mag an diesen Figuren (Fig. 8 u. 9).
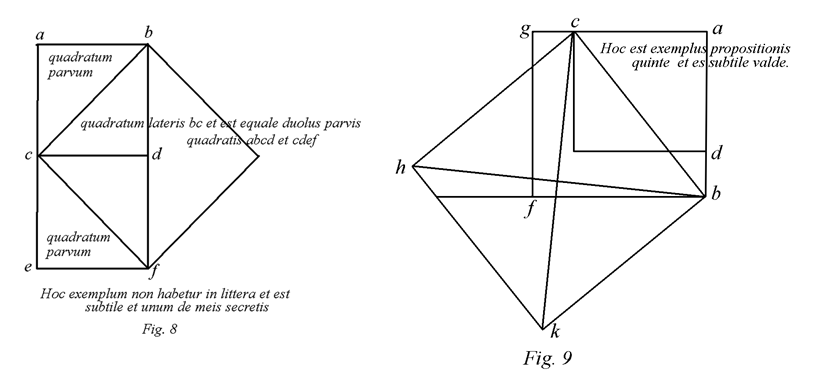
Auf den ersten Blick sind die beiden Figuren, insbesondere Fig. 9, etwas undurchsichtig. Bei genauerem Betrachten sieht man aber, dass in Fig. 8 die Seite cb die Hypotenuse und die Seiten bd und cd die Katheten des gleichschenkligen rechtwinkligen Dreiecks sind. In Fig. 9 ist die Seite bc die Hypotenuse und die Seiten ab und ac die Katheten des ungleichseitigen rechtwinkligen Dreiecks.
Der Satz des Pythagoras (a² + b² = c²) wird in der Geometria Culmensis nicht explizit genannt. Er wird aber zur Bestimmung des Mitteldreboms (Höhe) von gleichschenkligen und gleichseitigen Dreiecken angewendet, dabei wird in diesem Zusammenhang auch ein Verfahren zur Bestimmung der Quadratwurzel thematisiert.
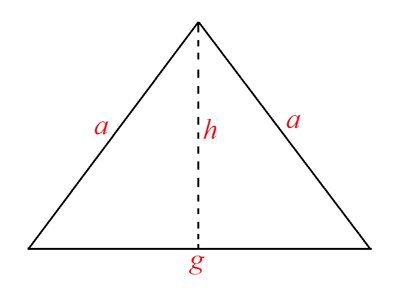
Bei gleichschenkligen Dreiecken muß zur rechnerischen Ermittlung des Mitteldreboms neben der Grundseite g auch die Länge der Schenkel gemessen sein. Der Mitteldrebom h kann dann folgendermaßen berechnet werden: ![]() . Für die Fläche gilt A = g∙h/2. Beispiel: a = 25; g = 30
. Für die Fläche gilt A = g∙h/2. Beispiel: a = 25; g = 30 ![]()
Für die Fläche ergibt sich A = 30∙20/2 = 300
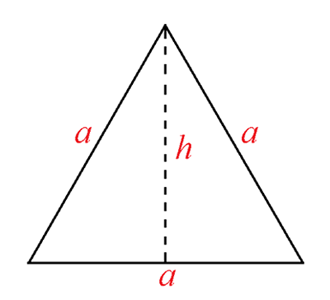
Entsprechend wird bei gleichseitigen Dreiecken verfahren. Für den Mitteldrebom gilt ![]()
Für die Fläche gilt hier A = a∙h/2.
Beispiel: a = 40![]()
und A ≈ 40∙34,6/2 = 692
Die häufigste Form von Dreiecken in der Praxis der Feldmessung sind ungleichseitige Dreiecke. Wenn der Mitteldrebom im Gelände abgelaufen werden kann, läßt er sich mit Hilfe eines Winkelkreuzes messen. Dazu soll man bei ungleichseitigen Dreiecken (alle drei Seiten verschieden) in der längsten Seite g den Punkt finden, der rechtwinklig gegen den gegenüberliegenden Winkel gerichtet ist und anschließend den Mitteldrebom h strecken (d.h. mit der Schnur oder der Kette ausmessen).
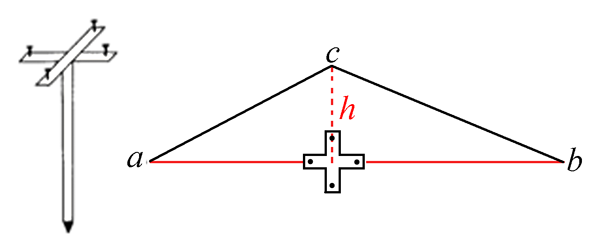
Das Winkelkreuz muss dabei so ausgerichtet werden, dass a und b waagrecht und der Fußpunkt des Winkelkreuzes und c senkrecht auf einer Linie liegen. Wird die Strecke vom Fußpunkt des Winkelkreuzes zu c gemessen erhält man die Höhe h des Dreiecks. Bei bekannter Entfernung von a nach b (Grundseite g) kann dann die Fläche des Dreiecks nach der Formel A = g∙h/2 berechnet werden.
Neben dem Winkelkreuz, mit dem sich rechte Winkel abstecken lassen, verwendeten die Feldmesser noch die Meßrute, in Ruten geteilte Seile oder Meßketten, ein hölzernes Winkelmaß (rechter Winkel) und ein Instrument zum Winkelmessen aus Holz. Letzteres bestand aus zwei beweglich gelagerten Schenkeln, die in abzählbare Grade geteilt waren; dazu gehörte ein langes, ebenfalls in Grade geteiltes Lineal (Regil) und ein zweites Lineal, das so lang war wie die beiden Schenkel des Instruments. Kann der Mitteldrebom nicht gestreckt werden, z.B. wegen der Gegebenheiten im Gelände, sollen die Feldmesser dieses Dreieck mit diesem Instrument in verkleinertem Maßstab abbilden und an ihm die Höhe messen. Der Verfasser der Geometria Culmensis bezieht sich hier auf die 5. Proposition des 6. Buches Euklids
4. Proposition: Zwei winkelgleiche Dreiecke haben die gleichen Seitenverhältnisse
5. Proposition: Umkehrung von Proposition 4

Das Dreieck auf dem Feld und das mit dem Meßwerkzeug abgebildete Dreieck sind sog. „ähnliche Dreiecke“, d.h. sie haben die gleichen Winkel und unterscheiden sich nur durch einen Proportionalitätsfaktor in den Seitenlängen. Hat man die Höhe auf dem abgebildeten Dreieck gemessen, kann man die Höhe des Dreiecks auf dem Feld bestimmen, indem man die gemessene Höhe des kleinen „ähnlichen“ Dreiecks mit dem Proportionalitätsfaktor multipliziert.
Wurden im Gelände die Seiten a = 20 Ruten, b = 12 Ruten und c = 24 Ruten eines Dreiecks gemessen, so kann dieses Dreieck mit dem Werkzeug in verkleinertem Maßstab abgebildet werden (1 Längeneinheit im kleinen Dreieck entspricht 1 Rute auf dem Feld). Mit dem zweiten Lineal kann dann die Höhe gemessen werden. Die Höhe h im kleinen Dreieck ist näherungsweise 10 (s. obige Abbildung). Die Höhe des Dreiecks im Gelände beträgt dann ungefähr 10 Ruten und die Fläche A ≈ 24∙10/2 = 120 Quadratruten (Tafeln). Die Skalierung auf den Schenkeln müsste eigentlich in der Mitte abgetragen werden, da der in der Mitte liegende Drehpunkt auch der Nullpunkt der Schenkel ist. Die Messergebnisse differieren aber nur geringfügig. Auch wird die Messung umso genauer, je größer das Meßwerkzeug ist.
Mit dem Satz von Heron kann die Fläche des Dreiecks exakt berechnet werden:![]() mit s = (a+b+c)/2 (Satz von Heron)
mit s = (a+b+c)/2 (Satz von Heron)
s = (20+12+24)/2 = 28 ![]()
Das entspricht ziemlich genau der näherungsweisen Berechnung. Auch wenn die Höhe im kleinen Dreieck etwas niedriger wie 10 LE (Längeneinheiten) ist, etwa 9,8 LE, erhält man eine gute Näherung.
Haben sie das Instrument zum Winkelmessen nicht zur Hand sollen die Feldmesser das Dreieck mit 3 Gerten (z.B. Haselnuß- oder Weidenruten) abbilden. Dazu werden zwei von diesen Gerten mit einem Nagel oder einer sonstigen Befestigung so zusammengefügt, dass man sie drehen kann. Mit der dritten Gerte wird dann das Dreieck zusammengefügt und mit einer vierten Gerte die Höhe gemessen, wobei alle Gerten mit der gleichen Maßeinteilung versehen sein müssen.
Zum Vergleich mit dem Meßverfahren aus der Geometria Culmensis ein Näherungsverfahren zur Flächenberechnung eines ungleichseitigen Dreiecks aus der im Jahre 1522 erschienenen Geometrey von Jacob Koebel.
Die Fläche eines ungleichseitigen Dreiecks sollte danach nach der Regel „(a+c)/2 multipliziert mit b/2“ berechnet werden, wobei a und c die beiden größten Seiten sind und b die kleinste. Es soll also die Fläche des Dreiecks ADE berechnet werden.
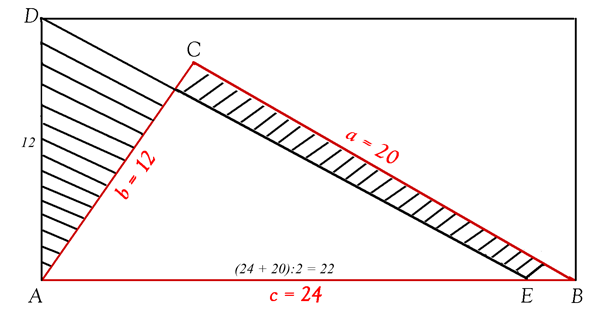
Wie man aus der Abbildung leicht erkennen kann, ist die zu wenig berechnete Fläche unterhalb der Seite a = 20 kleiner als die zuviel berechnete Fläche oberhalb der Seite b = 12. Deshalb ergibt sich hier für ein Dreieck mit den Seiten a = 20, b = 12 und c = 24 näherungsweise die Fläche A = 22∙12/2 = 132. Die berechnete Fläche ist also um etwa 10 % höher als die tatsächliche Fläche.
Diese Art von Feldmessung war für den das Flurstück bewirtschafteten Bauern nachteilig, da die tatsächliche Fläche kleiner war, als die nach dem Köbelschen Verfahren berechnete. Umgekehrt war sie für den Grundherren vorteilhaft, da sich ja die zu leistenden Zinsen und Abgaben auch nach der Flächengröße berechneten. Wie in der Vorrede der Geometria Culmensis nachzulesen ist, gab es auch in Preussen Zwietracht und Streit wegen fehlerhafter Feldmessung. Deshalb hat der Verfasser der Geometria Culmensis auf ausdrücklichen Wunsch des Hochmeisters Conrad von Jungingen die Aufgabe übernommen, ein Buch über die Erdmessung und deren Handhabung zu schreiben. Die Anleitungen in der Geometria Culmensis werden vermutlich auch zur erstaunlich hohen Entwicklung der Feldmesskunst im Ordensstaat um 1400 beigetragen haben.