Der Satz des Pythagoras wird in der Geometria Culmensis nicht explizit genannt. Er wird aber z.B. zur rechnerischen Bestimmung der Höhe von gleichschenkligen und gleichseitigen Dreiecken angewendet, wobei in diesem Zusammenhang auch ein Algorithmus (Verfahren) zur Bestimmung der Quadratwurzel thematisiert wird. Auch wird an zwei Figuren (Fig. 8 und Fig. 9 s. Dreiecke) der Zusammenhang zwischen den drei Seiten eines rechtwinkligen Dreiecks dargestellt.

Satzgruppe des Pythagoras
In einem Rechteck mit den Seitenlängen a und b teilt die Diagonale AB das Rechteck in zwei kongruente (deckungsgleiche) rechtwinklige Dreiecke. Unterteilt man das untere Dreieck nochmals in zwei rechtwinklige Dreiecke  mit der Höhe h und den Hypotenusenabschnitten p und q erhält man die drei „ähnlichen“ Dreiecke ABC, BC’D und AC’D; d.h. sie haben gleiche Winkel und die Seitenlängen unterscheiden sich jeweils nur um einen Proportionalitätsfaktor k_i.

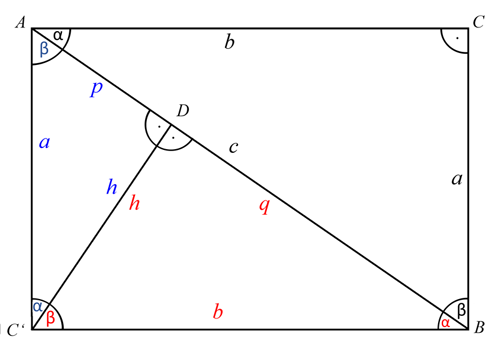
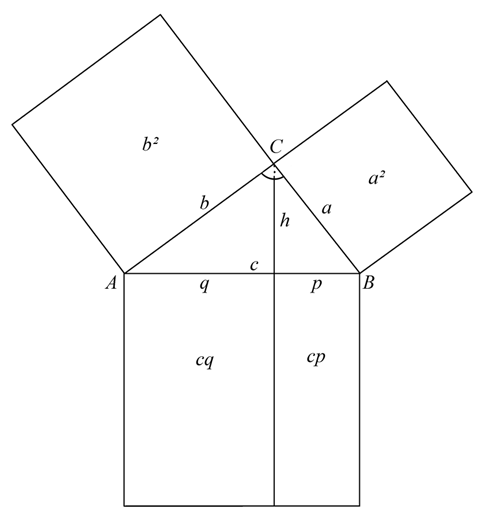
Legt man die drei Dreiecke übereinander ergibt sich folgendes Bild:

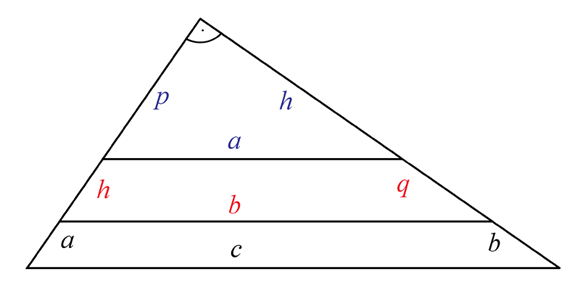
Das untere Dreieck hat die Seiten c, a und b, das mittlere die Seiten b, h und q und das obere Dreieck die Seiten a, p und h. Alle drei Dreiecke haben gleiche Winkel.
Es ergeben sich folgende Seitenverhältnisse:

– vom großen Dreieck zum mittleren Dreieck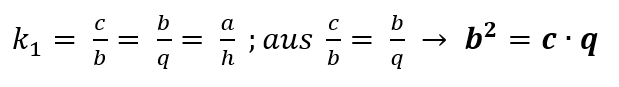

– vom großen Dreieck zum kleinen Dreieck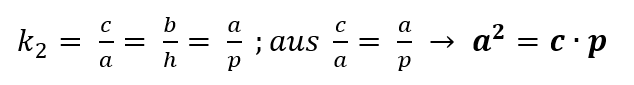

– vom mittleren Dreieck zum kleinen Dreieck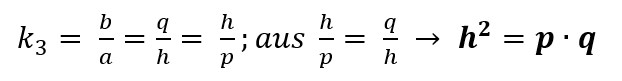

Kathetensatz des Euklid

Das Quadrat über a ist flächeninhaltsgleich zum Rechteck mit den Seiten c und p (a² = c∙p), und das Quadrat über b ist flächeninhaltsgleich zum Rechteck mit den Seiten c und q (b² = c∙q).

Höhensatz des Euklid

Das Quadrat über h ist flächeninhaltsgleich zum Rechteck mit den Seiten p und q (h² = p·q).

Addiert man a² = c·p und b² = c∙q ergibt sich unmittelbar der Satz des Pythagoras a² + b² = c∙p + c·q = c∙(p + q) = c²

Satz des Pythagoras

In einem rechtwinkligen Dreieck ist die Fläche des Quadrats über der Hypotenuse gleich der Summe der Flächen der Quadrate über den beiden Katheten (a² + b² = c²).

Auch die Berechnung der Fläche eines rechtwinkligen Dreiecks kann aus den Seitenverhältnissen der ähnlichen Dreiecke abgeleitet werden. Aus 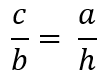(aus k₁) bzw. 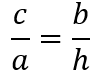(aus k₂) folgt .

Durch Scherung entlang der zur Grundseite c parallel verlaufenden Geraden durch Punkt C lässt sich das Dreieck ABC in ein flächengleiches Dreieck ABC‘ überführen. Die Diagonale AC‘ teilt das Rechteck mit den Seitenlängen c und h in zwei gleich große Dreiecke mit dem Flächeninhalt 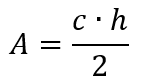. Das Rechteck ADBC wird durch die Diagonale c in zwei gleich große Dreiecke mit dem Flächeninhalt geteilt. Die Fläche eines rechtwinkligen Dreiecks ergibt sich also als oder .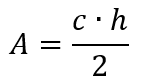

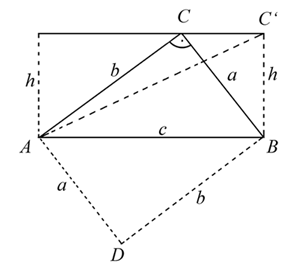
Mit der Formel lässt sich der Flächeninhalt eines beliebigen Dreiecks mit der Grundseite g und dem Abstand h zum g gegenüberliegenden Dreieckspunkt berechnen. Die Formel kann nur bei rechtwinkligen Dreiecken angewendet werden, wobei die beiden Katheten a und b den rechten Winkel einschließen.

Dazu kann man in der Geometria Culmensis folgendes nachlesen: