Sehnentafeln

Im Mittelalter benutzte man zur Bestimmung der Beziehungen zwischen Seiten und Winkeln von Dreiecken nicht wie heute die Sinus-Funktion sondern die Chord-Funktion. Wie der sinus ist auch chord ein Längenverhältnis  am Kreis, nämlich das Verhältnis von Sehnenlänge s und Kreisradius r zum Winkel α, den der Mittelpunkt dieses Kreises mit den Endpunkten der Sehne einschließt.

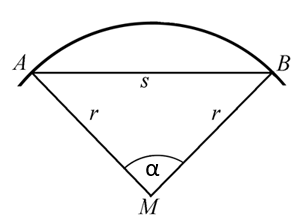
Jedem Winkel α ist ein bestimmtes Verhältnis von s : r zugeordnet, das von sogenannten Chordentafeln (Chord bedeutet Sehne), die schon seit der Antike bekannt sind, abgelesen werden kann. Zum Erstellen dieser Tafeln war ohne die modernen elektronischen Werkzeuge ein immenser Rechenaufwand erforderlich. Wenn man s und r kennt, kann nach Berechnung des Quotienten s : r aus der Sehnentafel der zugehörige Winkel abgelesen werden. Bevor in der zweiten Hälfte des 20. Jahrhunderts die elektronischen Taschenrechner aufkamen, wurden auch bei der Sinus-Funktion (Verhältnis von Gegenkathete zur Hypotenuse)  zur Winkelbestimmung Sinustafeln verwendet.

Heute können wir z.B. mit Hilfe eines Taschenrechners oder einem Tabellenkalkulationsprogramm über die Beziehung  chord(α) = 2∙ sin(α/2) leicht selbst solche Sehnentafeln erstellen. Will man den Winkel in Grad eingeben, muß beim Taschenrechner in den Einstellungen Grad (Degree) statt Bogenmaß (Radian) ausgewählt werden. Wenn beim Tabellenkalkulationsprogramm als Argument für die Sinus-Funktion der Winkel im Bogenmaß angegeben werden muß, läßt sich das Bogenmaß nach der Formel α_rad = (α_Grad / 180°) · π berechnen.

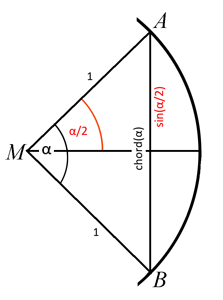
Eine Sehnentafel für  Winkel von α = 1° bis α = 90° ist hier zu finden.

Manche Feldmesser benutzten solche Sehnentafeln zur Winkelmessung noch im 19. Jahrhundert. Sie waren sehr umfangreich (ca. 70 Seiten) und man konnte daraus für jeden Chordwert den Winkel ablesen, sogar bis auf Minuten und Sekunden genau.