Winkelmessung
Für die Feldmesser gehörte es zum Alltag, Winkel auf dem Feld zu messen. War der Winkel auf dem Feld abgesteckt, konnte dessen Größe bestimmt werden. Dazu legte man die Schenkel des Instruments zum Winkelmessen (s. Dreiecksmessung) auf die beiden Grenzlinien und hat dann mit dem Lineal die Entfernung s zwischen den Schenkeln bei gleichem Abstand r zum Scheitelpunkt B gemessen. Der Chordwert, das Verhältnis von s : r, konnte dann berechnet werden und der zugehörige Winkel aus einer Sehnentafel (s. Sehnentafeln) abgelesen werden.
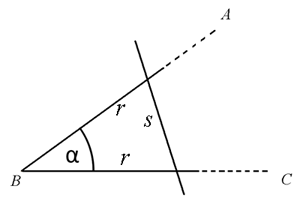
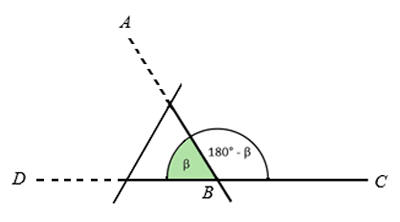
Die beiden Schenkel des Instruments zum Winkelmessen sollten nach dem Verfasser der Geometria Culmensis in 60 Gradus und das Lineal in 90 Gradus geteilt sein. Das Verhältnis von Sehne und Radius konnte damit maximal 90 : 60 = 1,5 werden. Das reichte aus, um damit Winkel zwischen 0° und 90° zu messen (chord(90°) = 1,41421…). Ist der Winkel![]() ABC größer als 90° kann der zugehörige Nebenwinkel β gemessen werden. Wird das Resultat von 180° subtrahiert, ergibt die Differenz den gesuchten Winkel
ABC größer als 90° kann der zugehörige Nebenwinkel β gemessen werden. Wird das Resultat von 180° subtrahiert, ergibt die Differenz den gesuchten Winkel ![]() ABC.
ABC.
Die kleinsten Längenmaße waren damals Fingerbreit (ca. 1,8 cm) und Handbreit (ca. 7,2 cm). Vier Fingerbreit machten eine Handbreit und 4 Handbreit machten einen Fuß. Wurden die Schenkel und das Lineal in Fingerbreit geteilt, waren die Schenkel bei 60 Fingerbreit etwas über einen Meter und das Lineal bei 90 Fingerbreit etwa 1 ½ Meter lang. Die Genauigkeit der Messung wird wohl davon abhängig gewesen sein wie gut die beiden Punkte A und C mit dem Instrument vom Punkt B aus anvisiert werden konnten. Auch die Länge des Instruments dürfte die Meßgenauigkeit beeinflußt haben.
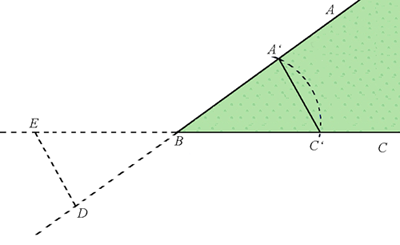
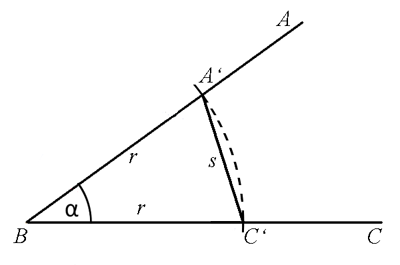
Zu vermutlich besseren Ergebnissen kommt man, wenn man von B mit Hilfe von Fluchtstäben in Richtung nach A mit möglichster Genauigkeit eine festgelegte Strecke abmisst (Punkt A‘ bzw. r). Ebenso verfährt man dann von B in Richtung nach C (Punkt C‘).
Anschließend wird die Sehne A’C‘ (s) gemessen, der Chordwert berechnet und der Winkel aus der Sehnentafel abgelesen.
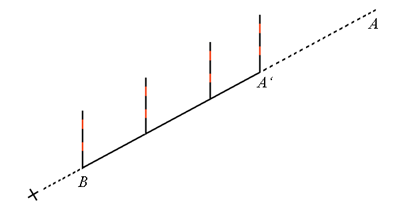
Die Fluchtstäbe werden dabei auf der Strecke BA‘ so aufgestellt, dass ein Beobachter (x) , der in Verlängerung der Fluchtlinie steht, nur den ersten Stab der Reihe sieht. Ebenso verfährt man mit der Strecke BC‘.
Etwas schwieriger wird es , wenn die örtlichen Gegebenheiten es nicht zulassen, die Strecken direkt zu messen. So kann z.B. der Winkel ![]() ABC einen Wald umfassen, sodass für die Strecke A’C‘ eine Schneise in den Wald gehauen werden müsste. Diesen Flurschaden möchte man aber vermeiden. In diesem Fall kann man den Winkel dadurch messen, dass die beiden Schenkel rückwärts verlängert und der dadurch entstandene (gleiche) Scheitelwinkel
ABC einen Wald umfassen, sodass für die Strecke A’C‘ eine Schneise in den Wald gehauen werden müsste. Diesen Flurschaden möchte man aber vermeiden. In diesem Fall kann man den Winkel dadurch messen, dass die beiden Schenkel rückwärts verlängert und der dadurch entstandene (gleiche) Scheitelwinkel ![]() DBE gemessen wird.
DBE gemessen wird.