Ein Näherungsverfahren zur Wurzelberechnung

In der Geometria Culmensis wird die Suche nach der Quadratwurzel einer vorgelegten Zahl zusammengefaßt folgendermaßen beschrieben:

Wie der Algorithmus spricht, so soll man von der vorgelegten Zahl gegen die linke Hand finden eine Zahl, und die heißt Fingerzahl, und ist eine Zahl unter zehn. Die ins Quadrat geführt soll die vorgelegte Zahl die über ihr steht ganz aufnehmen, oder ihr am nächsten kommen. Und was vorher geschrieben steht in dem Algorithmus ist hier zu lang zu setzen und auszusprechen.Wenn man die ins Quadrat geführte Zahl gefunden hat, die die vorgelegte Zahl ganz aufnimmt oder ihr am nächsten kommt so bleibet etwas über von der vorgelegten Zahl oder nicht. Mit dem Übrigen mache folgendes: die übrige Zahl, die da kein ganzes bringt, die soll sein der Zähler der Teile, und die  Wurzel, die man gefunden hat, die soll man verdoppeln, das wird dann der Nenner der Teile.

Das Verfahren (der Algorithmus) zur Wurzelberechnung wird im Buch zwar thematisiert, aber nicht ausführlich dargestellt. Insbesondere wird nicht klar, wie es weitergehen soll, wenn die „Fingerzahl“ gefunden wurde. Deshalb möchte ich hier etwas näher darauf eingehen.

Fingerzahlen sind die Zahlen 1, 2, … , 8, 9  und deren Quadrate entsprechend 1, 4, … , 64, 81. Wenn die quadrierte Fingerzahl die über ihr stehende Zahl ganz aufnehmen oder ihr am nächsten kommen soll, kann die über ihr stehende Zahl max. 2-stellig sein. Wenn man nun die Zahl z, aus der die Quadratwurzel gesucht ist, in zwei Blöcke aufteilt, einen linken Block für die quadrierte Fingerzahl und einen rechten Block dessen Ziffern durch Nullwerte ersetzt werden, kann daraus ein Startwert (erster Schätzwert für die Quadratwurzel) ermittelt werden. Ist die Anzahl Ziffern der Zahl z ungerade ist der linke Block 1-stellig, sonst 2-stellig. Der rechte Block hat dann in jedem Fall eine gerade Anzahl von Nullwerten. Daraus lässt sich leicht die Wurzel ziehen. Wenn man die Fingerzahl aus dem linken Block mit der Wurzel aus dem rechten Block multipliziert, erhält man einen ersten Näherungswert (Startwert)  a für die Wurzel aus z.

Bsp. 1: z = 172634 (gerade Anzahl von Ziffern).

Teilt man die Zahl z in einen linken Block, der die ersten zwei Ziffern enthält und einen rechten Block dessen Ziffern durch 0 ersetzt werden erhält man 17|0000. Wir suchen nun im linken Block die größte ganze Zahl, deren Quadrat kleiner oder gleich 17 ist und das ist die 4, denn 4² = 16 und 5² = 25. Mit a² =160000 und a = √16|0000 = √(4²∙10⁴) = 4∙10² = 400 erhält man einen ersten Schätzwert a für die Wurzel aus z.

Nachdem der Startwert a gefunden ist zerlegen wir die Quadratwurzel √z in einen Teil a und einen  Teil b für die gilt z = (a+b)² = a² + 2ab + b² und √z = a+b. Ziehen wir a² von z ab, verbleibt ein Rest r von 2ab + b². Unter Vernachlässigung von b² ergibt sich dann r = 2ab und ein Näherungswert für b ist dann r/(2a). Ist b größer als 1 wird a um den ganzzahligen Anteil von b erhöht und das Verfahren mit dem neuen a wiederholt. Wenn  b = r/(2a)  <1 (und r>=0) ist die größte Zahl a, deren Quadrat kleiner oder gleich z ist, gefunden und das Verfahren ist beendet. Der gesuchte Näherungswert für die Wurzel ist dann √z ≈  a + r/(2a), wobei der Bruch r/(2a) der nicht ganzzahlige Anteil an der Wurzel ist.

Im Bsp. 1: z = 172634

1. Näherung
   172634
 -160000   a²    ( a = 400)
——————
   12634 =  r;   b= r/2a = 12634/(2*400) = 15,…

2. Näherung
  172634
 -172225   a²    ( a = 415)
——————
      409 =  r;   b= r/2a = 409/(2*415)  < 1

Da b < 1 ist das Verfahren beendet und wir haben mit r/(2a) = 409/830 einen Näherungwert für den nicht-ganzzahligen Anteil der Wurzel. Mit 415^409/830 erhalten wir eine gute Näherung für die gesuchte Wurzel [(415^409/830)² = 172634,2428].

Bsp. 2:  z = 58239 (ungerade Anzahl von Ziffern).

Da die Anzahl Ziffern von z ungerade ist, ist der linke Block einstellig. Für eine erste Näherung ersetzen wir die vier letzten Ziffern jeweils durch eine 0 und erhalten dann 5|0000. Wir suchen nun die größte ganze Zahl, deren Quadrat kleiner oder gleich 5 ist und das ist die 2, denn 2² = 4 und 3² = 9. Als ersten  Schätzwert für die Wurzel erhalten wir dann  a = √40000 = √(4*10⁴) = 2*10² = 200 und a² = 200² = 40000.

1. Näherung
  58239
 -40000   a²    ( a = 200)
——————
   18239   r   b= r/2a = 18239/(2*200) = 45,….

2. Näherung
   58239
 – 60025   (a+b)²    ( a + b = 245)
——————
   -1786   r 

Der Rest r = -1786 ist negativ, deshalb ist 245² zu  groß. Hier macht sich nun die Vernachlässigung von b² bemerkbar. Wir reduzieren deshalb b = 45 schrittweise um 1 bis r positiv wird.

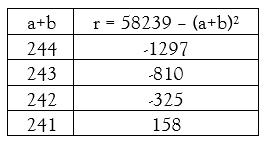
Für b= 41 wird r = 58239 – (240 + 41)² = 158 (positiv). Wir setzen nun a = 241 und errechnen wieder das neue b = r/(2a) = 158/(2*241) = 158/482. Da b < 1 ist das Verfahren beendet und wir haben mit r/(2a) = 158/482 einen Näherungwert für den nicht-ganzzahligen Anteil der Wurzel erhalten. Mit 241^158/482 erhalten wir eine gute Näherung für die gesuchte Wurzel [(241^158/482)² = 58239,10745].

Weitere Informationen und Beispiele zum Verfahren finden sich im Anhang des Buches.

Diejenigen, die sich schon einmal mit der Programmierung beschäftigt haben, werden vermutlich erkannt haben, dass sich dieser Algorithmus gut als Programmierübung eignet. Die Herausforderung besteht darin, auch Fälle, die zu Programmfehlern führen können (hier r < 0) abzufangen.

Ich habe das Programm der Einfachheit halber in VBA für Excel umgesetzt. Es ist hier zu finden. Es sind zwar einige Visual Basic (VB) spezifische Funktionen verwendet worden, die Umsetzung kann aber auch mit anderen Programmiersprachen erfolgen.